Atomic Structure Formulas

1. ThomsonΓÇÖs model of an atom

Entire mass and positive charge of an atom is uniformly distributed in a sphere of radius about 10^-10 m and negatively charged electrons are embedded in the sphere.

2. RutherfordΓÇÖs model of an atom

Entire mass, positive charge of an atom are concentrated in a very small j region of radius about 10^-15m, called nucleus. Electrons revolve round this nucleus in circular orbits.

3. Rutherford scattering, impact parameter and distance of closest approach

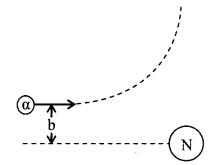
(i) The relation between the number of ╬▒-particles scattered N (╬╕) and the angle of scattering ╬╕ is
N(╬╕) Γê¥ cosec⁴ (╬╕/2)

(ii) Impact parameter
b = \(\frac{2 \mathrm{Ze}^{2} \cot (\theta / 2)}{4 \pi \varepsilon_{0} \mathrm{mv}_{0}^{2}}=\frac{\mathrm{kZe}^{2} \cot (\theta / 2)}{\mathrm{E}}\)

(iii) Distance of closest approach, If b = 0
r₀ = \(\frac{2 \mathrm{Zeq}}{4 \pi \varepsilon_{0} \mathrm{mv}_{0}^{2}}=\frac{2(\mathrm{Ze})(2 \mathrm{e})}{4 \pi \varepsilon_{0} \mathrm{mv}_{0}^{2}}=\frac{\mathrm{k} 2 \mathrm{Ze}^{2}}{\mathrm{E}}\)
E = Kinetic energy of a particle

4. BohrΓÇÖs model of an atom

(i) Electrons revolve round the nucleus in circular orbits of constant energy.
Centripetal force = Coulomb force
\(\frac{m v^{2}}{r}=k \frac{Z e^{2}}{r^{2}}\)

(ii) The orbits in which the angular momentum of an electron is integral multiple h/2╧Ç, are stable orbits. (Bohr’s quantum condition)
L = mvr = \(\frac{n h}{2 \pi}\)

(iii) A photon is emitted or absorbed due to transition of an electron from one energy level to another energy level. Thus
E₂ – E₁ = h╬╜ (in emission)
or E₁ – E₂ = h╬╜ (in absorption)
(Bohr’s frequency condition)

5. State of an electron in an atom

(i) The radius of n-th orbit:
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} m K e^{2} Z}\)
= \(a_{0} \frac{n^{2}}{Z}\)

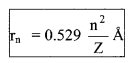
r_n ∝ \(\frac{n^{2}}{Z}\)

(ii) The velocity of electron in n-th orbit:
v_n = \(\frac{2 \pi \mathrm{Ke}^{2} \mathrm{Z}}{\mathrm{nh}}\)
= 2.188 x 10⁶ \(\frac{\mathrm{Z}}{\mathrm{n}}\) m/s
= \(\frac{c}{137}\left(\frac{Z}{n}\right)\)
v_n ∝ \(\frac{\mathrm{Z}}{\mathrm{n}}\)
For hydrogen

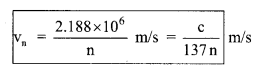
(iii) The period of an electron in n-th orbit
T_n = \(\frac{2 \pi r_{n}}{v_{n}}=\frac{n^{3} h^{3}}{4 \pi^{2} K^{2} m c^{4} Z^{2}}\) sec, T_n ∝ \(\frac{\mathrm{n}^{3}}{\mathrm{Z}^{2}}\)

(iv) Energy of an electron in n-th orbit (in hydrogen atom) For a BohrΓÇÖs atom of atomic number Z:
(a) Kinetic energy KE = \(\frac{\mathrm{KZe}^{2}}{2 \mathrm{r}_{\mathrm{n}}}=\frac{\mathrm{R} \mathrm{ch} \mathrm{Z}^{2}}{\mathrm{n}^{2}}, \mathrm{KE} \propto \frac{\mathrm{Z}^{2}}{\mathrm{n}^{2}}\)

(b) Potential energy U = \(-\frac{\mathrm{KZe}^{2}}{\mathrm{r}_{\mathrm{n}}}=-\frac{2 \mathrm{R} \mathrm{ch} \mathrm{Z}^{2}}{\mathrm{n}^{2}}, \mathrm{U} \propto \frac{\mathrm{Z}^{2}}{\mathrm{n}^{2}}\)

(c) Total energy

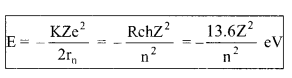
E ∝ \(\frac{Z^{2}}{n^{2}}\)

(d) Binding Energy B.E. = \(\frac{13.6}{n^{2}}\) Z² eV
BE ∝\(\frac{Z^{2}}{n^{2}}\)

6. Energy, frequency and wave number of emitted or abosrbed photons by an atom

(a) Energy of photon
h╬╜ = (E_n2 – E_n1)
= \(\frac{2 \pi^{2} \mathrm{K}^{2} \mathrm{me}^{4}}{\mathrm{h}^{2}}\left[\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]\)

(b) Frequency of photon
\(\bar{v}=\frac{2 \pi^{2} K^{2} m e^{4}}{h^{3}}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)

(c) Wave number

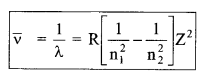
Z = 1 for H-atom
Where R is Rydberg constant
R = \(\frac{2 \pi^{2} K^{2} m e^{4}}{c h^{3}}\) = 1.1 ├ù 10⁷ m^-1
For a Bohr atom of atomic number

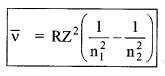
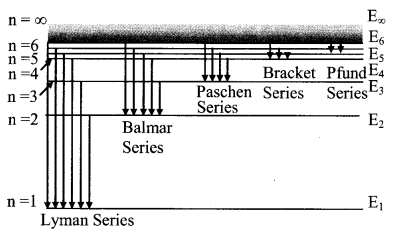
7. Various series of hydrogen spectrum

(i) Lyman series (in ultra violet region)
\(\bar{v}=\frac{1}{\lambda}=R\left[\frac{1}{1^{2}}-\frac{1}{n_{2}^{2}}\right]\), n₂ = 2, 3, 4……….
Minimum wavelength λ_min = 912 Å

(ii) Balmar Series (In visible region)
\(\vec{v}=\frac{1}{\lambda}=R\left[\frac{1}{2^{2}}-\frac{1}{n_{2}^{2}}\right]\), n₂ = 3, 4, 5 ………….
Minimum wavelength λ_min = 3645 Å

(iii) Paschen series (Infra red region)
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right]\), n₂ = 4, 5, 6…….
Minimum wavelength λ_min = 8210 Å

(iv) Brackett series
n₁ = 4 and n₂ = 5, 6, 7……….

(v) Pfund series
n₁ = 5 and n₂ = 6, 7, 8………

(vi) If an electron transition takes place from n-th orbit, then maximum number of lines m the spectrum = \(\frac{n(n-1)}{2}\)

8. Ioniztion and excitation energies, ionization and excitation potentials

Ionization energy = (E_Γê₧ – E_n) eV
Excitation energy = (E_n+1 – E_n) eV
Ionization Potential = (E_Γê₧ – E_n) V
Excitation Potential = (E_n+1 – E_n) V

9. Quantum numbers

• Principal quantum number (n): possible values of n = 1, 2, 3…….
• Orbital quantum number (l): possible values from 0 to (n – 1).
• Orbital magnetic quantum number (m₁): possible values are (2l + 1) integral from -l to +l.
• Spin quantum number (s) – possible values are (+\(\frac{1}{2}\)) and (-\(\frac{1}{2}\))

Orbital angular momentum = \(\frac{h}{2 \pi} \sqrt{l(l+1)}\)
Spin angular momentum = \(\frac{h}{2 \pi} \sqrt{s(s+1)}\)

10. Numbers of electrons

• Maximum number of electrons in an orbit 2n².
• Maximum number of electrons in a sub-orbit = 2(2l + 1)

11. PauliΓÇÖs exclusion principle
No two electrons in an atom can have the same set of four quantum numbers.

Visit the online portal Physicscalc.Com to understand the concepts of Physics much better and clarify your ambiguities.