Circular Motion Formulas

1. Circular motion

(a) angle(in radians) = \(\frac{\text { arc }}{\text { radius }}\)
or Δθ = \(\frac{\Delta \mathrm{S}}{\mathrm{r}}\) π rad. = 180°

(b) Angular velocity (\(\vec{\omega}\))
1. Instantaneous ω = \(\frac{d \theta}{d t}\)
2. Average \(\vec{\omega}_{\mathrm{av}}=\frac{\text { total angular displacement }}{\text { total time taken }}=\frac{\Delta \theta}{\Delta \mathrm{t}}\)
if v → linear velocity
α → angular acceleration
a → linear acceleration

(c) v = rω and \(\overrightarrow{\mathrm{v}}=\vec{\omega} \times \overrightarrow{\mathrm{r}}\)

(d) α = \(\frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\) or α = ω\(\frac{\mathrm{d} \omega}{\mathrm{d} \theta}\)

(e) a = ╬▒ r and \(\vec{a}=\vec{\alpha} \times \vec{r}\)

2. Newtons equation in circular motion

╧ë = ╧ë₀ + ╬▒ t
╬╕ = ╧ë₀ t + \(\frac{1}{2}\) ╬▒ t²
╧ë² = ╧ë₀² + 2 ╬▒ ╬╕

3. Centripetal force

F_c = \(\frac{m v^{2}}{r}\) = m╧ë²r = m╧ëv
a_c = \(\frac{v^{2}}{r}\) In vector \(\overrightarrow{\mathrm{F}}_{\mathrm{c}}=\mathrm{m}(\vec{\omega} \times \overrightarrow{\mathrm{v}})\)

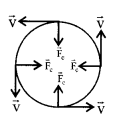
4. Net acceleration

\(\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{a}}_{\mathrm{c}}+\overrightarrow{\mathrm{a}}_{\mathrm{t}}\)

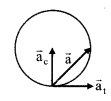
a_t → Tangential acceleration,
a_c → Centripetal acceleration anct
a_net = \(\sqrt{a_{t}^{2}+a_{c}^{2}}\)
a_c = \(\frac{v^{2}}{r}\) = ╧ë²r = v╧ë; a_t = \(\frac{d v}{d t}=\frac{d^{2} r}{d t^{2}}=\frac{v d v}{d x}\) = r╬▒

5. Motion in horizontal circle (conical pendulum)

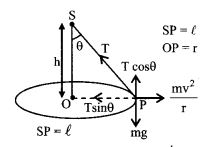
T cos ╬╕ = mg
T sin ╬╕ = mv²/r; tan ╬╕ = \(\frac{v^{2}}{r g}\)
tension T = mg \(\sqrt{1+\frac{v^{4}}{r^{2} g^{2}}}\)
The time period of revolution
T = \(2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}}=2 \pi \sqrt{\frac{l \cos \theta}{\mathrm{g}}}\)

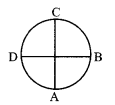
6. Vertical circular motion in case of string

(a) Tension at the lowest point A
T_A = \(\frac{m v_{A}^{2}}{\ell}\) + mg

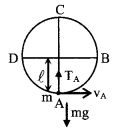
(b) Tension at point C
T_C = \(\frac{m v_{C}^{2}}{\ell}\) – mg
T_C = \(\frac{m v_{A}^{2}}{\ell}\) – 5 mg

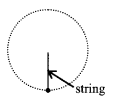
(c) Tension at point B
T_B = \(\frac{m v_{B}^{2}}{\ell}\)
T_B = \(\frac{m v_{A}^{2}}{\ell}\) – 2mg
T_A – T_C = 6mg
T_A – T_B = 3 mg
Thus T_A > T_B > T_C

7. Critical velocity (v_C)

The minimum velocity at which the circular motion is possible.
v_C at A = \(\sqrt{5 \mathrm{g} \ell}\)
v_C at C = \(\sqrt{g l}\)
v_C at B = \(\sqrt{3 \mathrm{g} \ell}\)
In the case of a critical velocity
T_A = 6mg
T_C = 0
T_B = 3mg
Case
⇒ If v_A > \(\sqrt{5 \mathrm{g} \ell}\)
Tension in string never becomes zero, particle will continue the circular motion.

⇒ If v_A = \(\sqrt{5 \mathrm{g} \ell}\)
Tension at point C becomes zero particle will just complete the circle.

⇒ If \(\sqrt{2 \mathrm{g} \ell}<\mathrm{v}_{\mathrm{A}}<\sqrt{5 \mathrm{g} \ell}\)
Particle will not follow circular motion, Tension becomes zero somewhere : between points B and C.

⇒ If v_A = \(\sqrt{2 \mathrm{g} \ell}\)
Both velocity and tension becomes zero at B & D and particle will ! oscillate along semi-circular path.

⇒ If v_A < \(\sqrt{5 \mathrm{g} \ell}\)
Velocity becomes zero between A & B but tension will not be zero any where. Particle oscillate about the point A.

8. Vertical circular motion in case of massless rod

Critical velocity


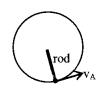
v_C at A = \(\sqrt{4 \mathrm{g} \ell}\)
v_C at C = 0
v_C at B = \(\sqrt{2 \mathrm{g} \ell}\)
T_A = 5 mg
T_C = – mg
T_B = 2 mg

9. Banking of tracks

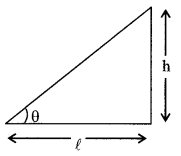
\(\frac{\mathrm{h}}{\ell}\) = tan ╬╕ = \(\frac{v^{2}}{r g}\), on frictionless road, banked by ╬╕
Maximum speed for skidding, on circular unbanked road V_max = \(\sqrt{\mu \mathrm{rg}}\)

You can witness plenty of concepts related to Physics not just Circular Motion from our site Physicscalc.Com during your preparation for quick help.