Conduction Formulas
You may feel the concept of Conduction extremely difficult to grasp. Not anymore! we have listed the Conduction Formulas to help you understand the concept much better. Master the Concept of Conduction and learn about the law of heat transfer through conduction, comparison of heat conduction with electrical conduction, etc. Ace up your preparation with our Physics Formulas Collection and clarify all your queries.
Conduction Formulae Sheet & Tables
1. Conduction
- In conduction. Molecules do not leave their position.
- The molecules transfer energy to the neighboring molecules due to mutual contact between them.
- The heat conduction i.e. transmission of heat in this mode occurs mainly in solids and mercury.
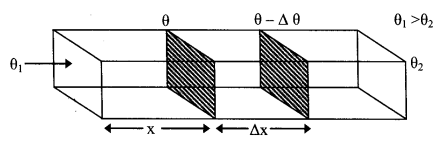
2. Law of heat transfer through conduction
rate of flow of heat \(\frac{\mathrm{dQ}}{\mathrm{dt}}=-\mathrm{KA} \frac{\mathrm{d} \theta}{\mathrm{dx}}\)
\(\frac{d \theta}{d x}\) → Temp, gradient
K → Coefficient of thermal conductivity conductivity
A → cross sectional Area
3. Comparison of heat conduction with electrical conduction
| Electrical Conduction | Thermal Conduction |
| 1. Electric charge flows from higher potential to lower potential | Heat flows from higher temperature to lower temperature |
| 2. The rate flow of charge is called electric current I = \( \frac{d q}{d t}\) |
The rate flow of heat is called electric current I = \( \frac{d Q}{d t}\) |
| 3. By Ohm’s law, I = \( \frac{V_{1}-V_{2}}{R}\) |
The thermal current is I = \( \frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{R}_{\mathrm{Th}}}\) |
| 4. The electrical resistance is given by R = \( \rho \frac{\ell}{\mathrm{A}}=\frac{\ell}{\sigma \mathrm{A}}\) Where ρ is resistivity and a is conducitividy |
The thermal resistance is given by \( \mathrm{R}_{\mathrm{Th}}=\frac{\ell}{\mathrm{K} \mathrm{A}}\) where K is thermal conductivity of the conductor |
4. Combination of straight rods (Let ╬╕1 > ╬╕2)
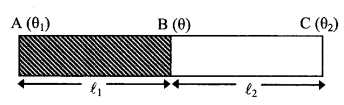
Heat current in Ist rod = \(\frac{\mathrm{K}_{1} \mathrm{A}\left(\theta_{1}-\theta\right)}{\ell_{1}}\) … (1)
Heat current in IIst rod = \(\frac{\mathrm{K}_{2} \mathrm{A}\left(\theta-\theta_{2}\right)}{\ell_{2}}\)
In steady state,
\(\frac{\mathrm{K}_{1} \mathrm{A}\left(\theta_{1}-\theta\right)}{\ell_{1}}=\frac{\mathrm{K}_{2} \mathrm{A}\left(\theta-\theta_{2}\right)}{\ell_{2}}\)
╬╕ = \(\frac{\mathrm{K}_{1} \ell_{2} \theta_{1}+\mathrm{K}_{2} \ell_{1} \theta_{2}}{\mathrm{K}_{1} \ell_{2}+\mathrm{K}_{2} \ell_{1}}\)
Keq = \(\frac{\ell_{1}+\ell_{2}}{\frac{\ell_{1}}{K_{1}}+\frac{\ell_{2}}{K_{2}}}\)
5. Parallel combination
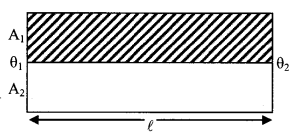
Let \(\frac{\mathrm{d} \mathrm{H}_{1}}{\mathrm{dt}}\) and \(\frac{\mathrm{d} \mathrm{H}_{2}}{\mathrm{dt}}\) be the heat, conducted in first and second rod. The resultant of these is assumed to be \(\frac{\mathrm{d} \mathrm{H}}{\mathrm{dt}}\).
\(\frac{\mathrm{d} \mathrm{H}}{\mathrm{dt}}=\frac{\mathrm{d} \mathrm{H}_{1}}{\mathrm{dt}}+\frac{\mathrm{d} \mathrm{H}_{2}}{\mathrm{dt}}\)
= \(\frac{\mathrm{K}_{1} \mathrm{A}_{1}\left(\theta_{1}-\theta_{2}\right)}{\ell}+\frac{\mathrm{K}_{2} \mathrm{A}_{2}\left(\theta_{1}-\theta_{2}\right)}{\ell}\)
= \(\left(\frac{\mathrm{K}_{1} \mathrm{A}_{1}}{\ell}+\frac{\mathrm{K}_{2} \mathrm{A}_{2}}{\ell}\right)\)(╬╕1 – ╬╕2) …….(1)
Keq = \(\frac{\mathrm{K}_{1} \mathrm{A}_{1}+\mathrm{K}_{2} \mathrm{A}_{2}}{\mathrm{A}_{1}+\mathrm{A}_{2}}\)
Physicscalc.Com has been curated by experts as the sought after place for Formulas of Physics, Chemistry, Maths, etc.