Deviation and Dispersion Formulas

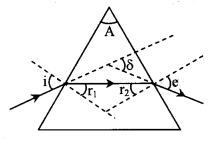
A → Angle of prism
δ → Angle of deviation
╬┤ = i + e – A
A = r₁ + r₂

1. Condition of no emergence

┬╡ > \(\frac{1}{\sin A / 2}\) > cosec(A/2)
Condition of Grazing Emergence (means = e = 90┬░)
r₂ = ╬╕_c
i = sin^-1 [\(\sqrt{\mu^{2}-1}\) sin A – cos A]
Condition of max. deviation
Deviation will be max. when i_max = 90┬░
╬┤_max = 90┬░ + sin^-1 [┬╡ sin (A – ╬╕_c)] – A
Condition for min. deviation
it occur when i = e, r₁ = r₂ = r & A = r/2
╬┤_min = (2i – A)

2. Prism formula

┬╡ = \(\frac{\sin \left(\frac{\delta_{\min }+A}{2}\right)}{\sin A / 2}=\frac{\sin \left(\frac{\delta_{\min }+A}{2}\right)}{\sin A / 2}\)
For thin prism
deviation ╬┤ = A(┬╡ – 1)

3. Dispersion

Splitting of a beam of white light into its constituent colours.

4. CauchyΓÇÖs formula

┬╡ = A + \(\frac{C}{\lambda^{4}}+\frac{C}{\lambda^{4}}\)
A, B & C are constants.

5. Angular dispersion

╬╕ = ╬┤_v – ╬┤_r = (┬╡_v – ┬╡_r) A

6. Dispersive power

\(\frac{\theta}{\delta_{y}}=\omega=\frac{\mu_{\mathrm{v}}-\mu_{\mathrm{r}}}{\mu_{\mathrm{y}}-1}=\frac{\Delta \mu}{\mu-1}\)

7. Conbination of prisms

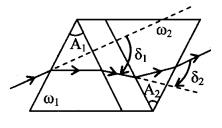
net deviation
╬┤ = ╬┤₁ – ╬┤₂
╬┤ = (┬╡₁ – 1) A₁ – (┬╡₂ – 1) A₂
net angular dispersion
╬┤_v – ╬┤_r = (┬╡_1v – ┬╡_1r) A₁ – (┬╡_2v – ┬╡_2r) A₂
= (┬╡_1y – 1)╧ë₁A₁ – (┬╡_2y – 1)╧ë₂A₂

8. Dispersion without deviation

╬┤_y = o, (┬╡_1y – 1) A₁ = (┬╡_2y – 1)A₂
╬┤_v – ╬┤_r = ╬┤₁ (╧ë₁ – ╧ë₂) = ╬┤₂ (╧ë₁ – ╧ë₂)

9. Average deviation without dispersion

╬┤_v – ╬┤_r = 0
(┬╡_1y – 1) ╧ë₁A₁ = (┬╡_2y – 1) ╧ë₂A₂
╬┤ = ╬┤₁\(\left(1-\frac{\omega_{1}}{\omega_{2}}\right)\)
╬┤₁ = (┬╡_1y – 1) A₁

Seek help regarding various concepts of physics that you feel difficult from the one-stop destination of formulas i.e. Physicscalc.Com