Electrostatics Formulas

1. Fundamental forces of nature

• Gravitational
• Electromagnetic,
• Nuclear,
• Weak.

Relative strength 1 : 10³⁶ : 10³⁹ : 10¹⁴
Charge is quantised, the quantum of charge is e = 1.6 × 10^-19 C.
Charge is conserved, invariant, additive

2. CoulombΓÇÖs law

\(\overrightarrow{\mathrm{F}}=\mathrm{K} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
K = \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 ├ù 10⁹\(\frac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}\)
╬╡₀ = 8.854 ├ù 10^-12\(\frac{C^{2}}{N m^{2}}\)
= Permittivity of free space
\(\frac{\varepsilon}{\varepsilon_{0}}\) = ╬╡_r = Relative permittivity or dielectric constant of a medium.
\(\overrightarrow{\mathrm{E}}=\frac{\mathrm{Kq}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)

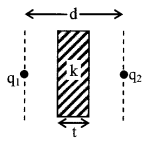
Note: – If a plate of thickness t and dielectric constant k is placed between the j two point charges lie at distance d in air then new force
\(\mathrm{F}=\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{4 \pi \varepsilon_{0}(\mathrm{d}-\mathrm{t}+\mathrm{t} \sqrt{\mathrm{k}})^{2}}\)
effective distance between the charges is
d’ = (d – t + t\(\sqrt{\mathrm{k}}\))

3. Intensity of electric field

\(\overrightarrow{\mathrm{E}}\) = Force on a unit positive charge = \(\frac{\overrightarrow{\mathrm{F}}}{\mathrm{q}_{0}}\) N/C or V/m.
Due to a point charge q intensity at a point of positive vector \(\overrightarrow{\mathrm{r}}\)
\(\overrightarrow{\mathrm{E}}=\frac{\mathrm{Kq}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)

4. Electric potential

Work done against the field to take a unit positive charge from infinity (reference point) to the given point.
V_P = – \(\int_{\infty}^{P} \vec{E} \cdot \overrightarrow{d r} \text { volt }\)
Due to a point charge q, potential
V =K \(\frac{q}{r}\) volt

5. Principle of superposition

Resultant force due to a number of charges
\(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_{1}+\overrightarrow{\mathrm{F}}_{2}+\ldots . .+\overrightarrow{\mathrm{F}}_{\mathrm{n}}\)
Resultant intensity of field
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}}_{1}+\overrightarrow{\mathrm{E}}_{2}+\ldots . . \overrightarrow{\mathrm{E}}_{\mathrm{n}}\)
Resultant potential V = V₁ + V₂ + … + V_n

6. Relation between \(\overrightarrow{\mathrm{E}}\) and V

\(\overrightarrow{\mathrm{E}}\) = – grad V = – \(\vec{\nabla} V=-\frac{\partial V}{\partial r} \hat{r}\)
In cartesian coordinates
\(\overrightarrow{\mathrm{E}}=-\left[\hat{\mathrm{i}} \frac{\partial \mathrm{V}}{\mathrm{dx}}+\hat{\mathrm{j}} \frac{\partial \mathrm{V}}{\partial \mathrm{y}}+\hat{\mathrm{k}} \frac{\partial \mathrm{V}}{\partial \mathrm{z}}\right]\)

7. Electric flux

Treating area element as a vector
d╬ª = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}\), ╬ª = \(\int_{s} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}\) volt – metre

8. GaussΓÇÖs theorem

Total outward flux through a closed surface = (4πK) times of charge enclosed
or Φ = \(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=4 \pi \mathrm{K} \sum \mathrm{q}=\frac{1}{\varepsilon_{0}} \Sigma \mathrm{q}\)

9. Intensity and potential due to a non-conducting charged sphere

\(\overrightarrow{\mathrm{E}}_{\text {out }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}, \mathrm{E}_{\text {out }} \propto \frac{1}{\mathrm{r}^{2}}\)
\(\overrightarrow{\mathrm{E}}_{\text {surface }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{R}^{2}} \hat{\mathrm{r}}\)
\(\overrightarrow{\mathrm{E}}_{\text {inside }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{R}^{3}} \overrightarrow{\mathrm{r}}, \quad \mathrm{E}_{\text {inside }} \propto \mathrm{r}\)

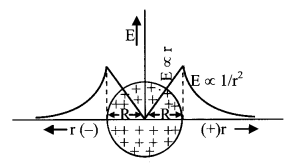
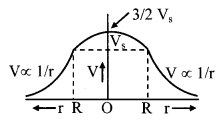
V_out = K \(\frac{Q}{r}\), V_surface = K \(\frac{Q}{r}\)
and V_inside = \(\frac{\mathrm{KQ}\left(3 \mathrm{R}^{2}-\mathrm{r}^{2}\right)}{2 \mathrm{R}^{3}}\)
V_centre = \(\frac{3}{2} \frac{\mathrm{KQ}}{\mathrm{R}}\) = 1.5 V_surface

10. Intensity and potential due to a conducting charged sphere

Whole charge comes out on the surface of the conductor.
\(\overrightarrow{\mathrm{E}}_{\text {out }}=\frac{1}{4 \pi \pi_{0}} \frac{\mathrm{Q}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\)
\(\overrightarrow{\mathrm{E}}_{\text {surface }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{R}^{2}} \hat{\mathrm{r}}\)
\(\overrightarrow{\mathrm{E}}_{\text {inside }}=0\)

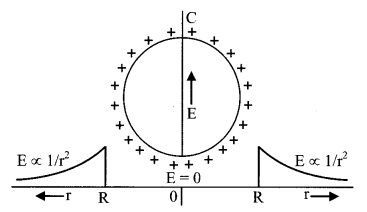
V_out = K\(\frac{Q}{r}\)
V_surface = K\(\frac{Q}{R}\)
V_inside = K\(\frac{Q}{R}\) (Constant)

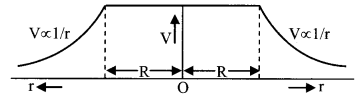
11. Electric potential and field intensity due to a charged ring

On axis
V = \(\frac{K Q}{\left(R^{2}+x^{2}\right)^{1 / 2}}\)
\(\overrightarrow{\mathrm{E}}=\frac{\mathrm{KQx}}{\left(\mathrm{R}^{2}+\mathrm{x}^{2}\right)^{3 / 2}} \hat{\mathrm{x}}\)

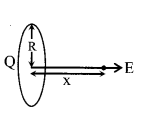
(x is the distance of the point on the axis from the centre)
At centre E = 0, V = \(\frac{\mathrm{KQ}}{\mathrm{R}}\)
Note: – If charged ring is semicircular then E.F. at the centre is
\(\frac{2 \mathrm{K} \lambda}{\mathrm{R}}=\frac{\mathrm{Q}}{2 \pi^{2} \mathrm{R}^{2} \varepsilon_{0}}\)
and potential V = \(\frac{\mathrm{KQ}}{\mathrm{R}}\)

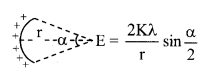
12. Electric field intensity due to very long (∞) line charge

\(\overrightarrow{\mathrm{E}}=\frac{2 \mathrm{K} \lambda}{\mathrm{r}} \hat{\mathrm{n}}=\frac{1}{2 \pi \varepsilon_{0}} \frac{\lambda}{\mathrm{r}} \hat{\mathrm{n}}\)
\(\hat{\mathrm{n}}\) is a unit vector iionpjd to line charge.

13. Electric field intensity due to a charged sheet having very large (∞) surface area

\(\overrightarrow{\mathrm{E}}\) = 2πK σ \(\hat{\mathrm{n}}\) (constant)
σ → charge of unit cross section

14. Electric field intensity due to an infinite charged conducting plate

\(\overrightarrow{\mathrm{E}}\) =4πKσ \(\hat{\mathrm{n}}=\frac{\sigma}{\varepsilon_{0}} \hat{\mathrm{n}}\)(constant)
σ → charge of unit surface area

15. Electric dipole

Two equal and opposite point charges separated by a small distance. Dipole moment \(\overrightarrow{\mathrm{p}}=\mathrm{q} \overrightarrow{\mathrm{d}}\). Direction of \(\overrightarrow{\mathrm{p}}\) is from -q to + q.

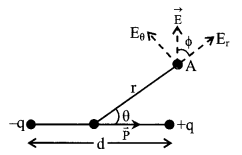
Potential at a point A (r, ╬╕)
V = \(\frac{\mathrm{Kqd} \cos \theta}{\mathrm{r}^{2}}\)
V = \(\frac{\mathrm{Kp} \cos \theta}{\mathrm{r}^{2}}=\mathrm{K} \frac{\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{r}}}{\mathrm{r}^{3}}\)

Electric field intensity

E = \(\frac{\mathrm{p}}{4 \pi \varepsilon_{0} \mathrm{r}^{3}} \sqrt{1+3 \cos ^{2} \theta}\)
E_r = 2K\(\left(\frac{\mathrm{p} \cos \theta}{\mathrm{r}^{3}}\right)\)
E_╬╕ = K \(\left(\frac{p \sin \theta}{r^{3}}\right)\)
E = \(\sqrt{\mathrm{E}_{\mathrm{r}}^{2}+\mathrm{E}_{\theta}^{2}}\)
On axis ╬╕ = 0, E_r = E = \(\frac{2 \mathrm{kp}}{\mathrm{r}^{3}}\)

On equatorial ╬╕ = \(\frac{\pi}{2}\), E_╬╕ = E = \(\frac{\mathrm{Kp}}{\mathrm{r}^{3}}\)
Angle between E.F. at point A and x – axis is (╬╕ + ╬ª)
where tan Φ = \(\frac{1}{2}\) tan θ

16. Dipole in an electric field

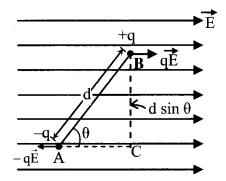
In a uniform field F_net = 0, (No translatory motion)
Torque \(\vec{\tau}=\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{E}}\) or τ = pE sin θ
Potential energy of dipole
U = – \(\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{E}}\)
(dipole perpendicular to field is taken as reference state). Work done in rotating the dipole from ╬╕₁ to ╬╕₂.
W = U₂ – U₁ = pE (cos ╬╕₁ – cos ╬╕₂)
Time period of oscillation of electric dipole in uniform E.F.
T = 2π\(\sqrt{\frac{I}{P . E}}\);
I = moment of inertia

17. Equilibrium of charged soap bubble

For a charged bubble
P_ext + P_elct. = \(\frac{4 \mathrm{T}}{\mathrm{r}}\)
For P_ext = 0, P_elct. = \(\frac{4 \mathrm{T}}{\mathrm{r}}\)
or \(\frac{\sigma^{2}}{2 \varepsilon_{0}}=\frac{4 T}{r}\)

Electric field on surface
E_surface = \(\left(\frac{8 \mathrm{T}}{\varepsilon_{0} \mathrm{r}}\right)^{1 / 2}\)
Potential on surface
V_surface = \(\left(\frac{8 \mathrm{Tr}}{\varepsilon_{0}}\right)^{1 / 2}\)

18. Energy density in electric field

U = \(\frac{1}{2}\) ╬╡₀E² (J/m³)

19. When small drops of charge q forms a big drops of charge Q

Q = nq, R = r n^1/3
V_big =n^2/3 V_small

20. Electric break-down or electric strength

Max. electric field can be created in the given medium.
For air E_max = 3 ├ù 10⁶ V/m

Seek help on various concepts taking the help of Formulas provided on the trusted portal Physicscalc.Com and clear all your ambiguities.