Motion in One Dimension Formulas

1. DISTANCE (s) (Scalar) = Total path cover

Length of path followed by particle = length of I path (See fig.)

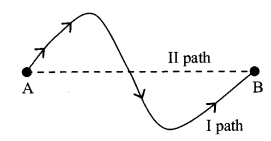
2. DISPLACEMENT (r) (Vector) = final position – initial position

Shortest Length of path followed by particle = length of II^nd path.
(See. fig.)

3. SPEED (scalar)

1. Instantaneous speed = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)

2. Average speed \(\overline{\mathrm{V}}=\frac{\text { Total dis tan ce }}{\text { Total time }}\)
\(\overline{\mathrm{V}}=\frac{s_{1}+s_{2}+\ldots . s_{n}}{t_{1}+t_{2}+\ldots . t_{n}}=\frac{s_{1}+s_{2}+\ldots s_{n}}{\frac{s_{1}}{V_{1}}+\frac{s_{2}}{V_{2}}+\ldots . . \frac{s_{n}}{V_{n}}}=\frac{V_{1} t_{1}+V_{2} t_{2}+\ldots \ldots . V_{n} t_{n}}{t_{1}+t_{2}+\ldots \ldots \ldots \ldots . t_{n}}\)

• If t₁ = t₂ = …… = t_n; \(\overline{\mathrm{V}}=\frac{V_{1}+V_{2}+\ldots \ldots+V_{n}}{n}\),
  for n = 2, \(\overline{\mathrm{V}}=\frac{V_{1}+V_{2}}{2}\)
• If s₁ = s₂ = …….. = s_n; \(\bar{V}=\frac{n}{\frac{1}{V_{1}}+\frac{1}{V_{2}}+\ldots \ldots \frac{1}{V_{n}}}\);
  in case n = 2 \(\overline{\mathrm{V}}=\frac{2 \mathrm{V}_{1} \mathrm{V}_{2}}{\mathrm{V}_{1}+\mathrm{V}_{2}}\)

4. VELOCITY \(\overrightarrow{\mathrm{V}}\) (vector)

1. Instantaneous velocity = \(\frac{\overrightarrow{\mathrm{dr}}}{\mathrm{dt}}\)

2. Average velocity = \(\frac{\text { Total displacement }}{\text { Total Time }}=\frac{\overrightarrow{\mathrm{r}}_{2}-\overrightarrow{\mathrm{r}}_{1}}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\frac{\Delta \overrightarrow{\mathrm{r}}}{\Delta t}\)
= \(\left|\vec{V}_{a v}\right|\) Γëñ \(\overline{\mathrm{V}}\)

5. FOR UNIFORM MOTION

• Distance= speed ├ù time
• Displacement = velocity ├ù time

FOR UNIFORM ACCELERATION WHEN \(\overrightarrow{\mathbf{a}}\) = CONST.

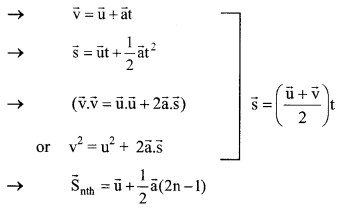
u → initial velocity, v → final velocity,
a → acceleration, s → displacement
Note:- Motion under gravity
v = u – \(\frac{1}{2}\)gt²
v² = u² – 2 gh
h_nth = u – \(\frac{1}{2}\) g(2n – 1)
(i) If a particle is thrown vertically upwards with initial velocity u then equation of motion becomes

• Maximum height attained by the particle = \(\frac{u^{2}}{2 g}\)
• Time to reach maximum height = \(\frac{\mathrm{u}}{\mathrm{g}}\)
• Time of flight = \(\frac{2 u}{g}\)

(ii) If a particle is thrown vertically downwards with initial velocity u then equation of motion becomes
v = u + gt
y =ut+ \(\frac{1}{2}\) gt²
v² = u² + 2 gy
y_nth = u+ \(\frac{1}{2}\)g(2n – 1)

6. ACCELERATION

1. Instantaneous acceleration
\(\overrightarrow{\mathrm{a}}=\frac{\mathrm{d} \overrightarrow{\mathrm{v}}}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \overrightarrow{\mathrm{r}}}{\mathrm{dt}^{2}}, \overrightarrow{\mathrm{a}}=\frac{\overrightarrow{\mathrm{v}} \overrightarrow{\mathrm{dv}}}{\mathrm{ds}}\)

2. Average acceleration
\(\vec{a}=\frac{\text { net change in velocity }}{\text { total time }}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\overrightarrow{\mathrm{v}}_{2}-\overrightarrow{\mathrm{v}}_{1}}{\mathrm{t}_{2}-\mathrm{t}_{1}}\)

7. DISTANCE COVERED

S = \(\int_{t_{1}}^{t_{2}}\)v dt = Area under the v – t curve and t axis, (see fig.)

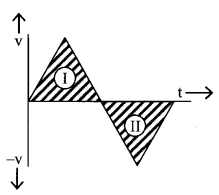
→ distance = Area I + Area II
ΓåÆ displacement = Area I – Area II

• If acceleration (a) is the function of time then
  Change in velocity = v₂ – v₁ = \(\int_{v_{1}}^{v_{2}}\) dv = \(\int_{t_{1}}^{t_{2}}\) adt = Area under the a – t curve and t axis.
• If acceleration (a) is the function of position (x) then
  \(\int_{v_{1}}^{v_{2}}\)vdv = \(\int_{x_{1}}^{x_{2}}\)adx

Take help from Physicscalc.Com and get different concepts formulas that you might need as a part of your work or assignments.