Unit and Dimension Formulas

Value Of Physical Quantity

Value of physical quantity = nu (u is unit and n is numeric)
nu = constant or n₁u₁ = n₂u₂ or

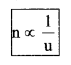
Fundamental Quantities

• Length = meter – L
• Mass = kilogram – M
• Time = second – T
• Electric current = ampere – A
• Temperature = kelvin, ┬░C – K, ╬╕
• Luminous intensity = candella – cd
• Amount of substance = mole – mol

Dimensional Formula

[M^a L^b T^c ╬╕^d]
Imp.
1. Always same dimensional quantities can be added or subtracted from each other
2. Measuring system

Conversion

From one system to another system
n₂ = n₁\(\left(\frac{M_{1}}{M_{2}}\right)^{a}\left(\frac{L_{1}}{L_{2}}\right)^{b}\left(\frac{T_{1}}{T_{2}}\right)^{c}\)

Absolute Error

╬öa = Apparent value – Real value
= a = a_o

Fractional error and percentage error

Relative error/fractional error = \(\frac{\Delta \mathbf{a}}{\mathrm{a}_{0}}\),
Percentage error = \(\frac{\Delta \mathbf{a}}{\mathrm{a}_{0}}\) × 100

Combination of errors

• If x = a + b ΓçÆ ╬öx = ╬öa + ╬öb
• x = a – b ΓçÆ ╬öx = ╬öa + ╬öb
• x = a/b ΓçÆ \(\frac{\Delta \mathrm{x}}{\mathrm{x}}=\frac{\Delta \mathrm{a}}{\mathrm{a}}+\frac{\Delta \mathrm{b}}{\mathrm{b}}\)
• x = aⁿ ΓçÆ \(\frac{\Delta \mathrm{x}}{\mathrm{x}}=\mathrm{n} \frac{\Delta \mathrm{a}}{\mathrm{a}}\)
• x = \(\frac{\mathrm{a}^{\mathrm{n}} \mathrm{b}^{\mathrm{m}}}{\mathrm{c}^{\mathrm{p}}}\) ΓçÆ \(\frac{\Delta \mathrm{x}}{\mathrm{x}}=\mathrm{n} \frac{\Delta \mathrm{a}}{\mathrm{a}}+\mathrm{m} \frac{\Delta \mathrm{b}}{\mathrm{b}}+\mathrm{p} \frac{\Delta \mathrm{c}}{\mathrm{c}}\) (maximum)
• x = log_ea ΓçÆ ╬öx = \(\frac{\Delta \mathrm{a}}{\mathrm{a}} \Rightarrow \frac{\Delta \mathrm{x}}{\mathrm{x}}=\frac{1}{\mathrm{x}} \frac{\Delta \mathrm{a}}{\mathrm{a}}\)

Common rules for counting signification

Rule 1.
All non zero digits are significant.
Ex. x = 1234 has four significant figures.

Rule 2.
All zero occurring between two non zero digits are significant
Ex. x = 1007 has four significant figure. Again x = 1.0809 has five significant figure

Rule 3.
In a number less than one, all zeros to the right of decimal point and to the left of a non zero digit are NOT significant.
Ex. x = 0.0084 has only two significant digits

Rule 4.
All zeros on the right of the last non zero digit in the decimal part are significant
Ex. x = 0.00800 has three significant figure 8, 0, 0. The zeros before 8 are not significant. Again 1.00 has three significant figures

Rule 5.
All zeros on the right of non zero digit are NOT significant.
Ex. x = 378000 has three significant figures

Rule 6.
All zeros on the right of the last non zero digit become significant, when they come from a measurement.
Ex. x = 3050 m. It has four significant figures.

Arthimetical operations with significant figures
(a) Addition and subtraction: –
In addition or subtraction, the number of decimal places in the result should equal the smallest number of decimal places of terms in the operation.

(b) Multiplication and Division: –
In multiplication and division, the number of significant figures in the product or in the quotients is the same as the smallest number of significant figures in any of the factors.
Ex. \(\frac{9500}{10.23}\) = 928.64125
As 9500 has minimum number of significant figures (i.e. 2), therefore, the quotient can have only two significant digits. On rounding off. we obtain the quotient = 930

Some of the non si units in common use are
(a) For length/distance

1. Astronomical unit	1 AU= 1.496 × 1011 m
2. Light year	1 ly = 9.64 × 1015 m
3. Parallactic second	1 pc = 3.084 × 1016 m = 3.26 ly
4. Micron or micrometer	1 ╬╝m = 10-6 m
5. Nanometer	1 nm = 10-9 m
6. Angstrom unit	1 Å = 10-10 m
7. X – ray unit	1 xu = 10-13 m
8. Fermi	1 f = 10-15 m
9. Yard	1 yd = 0.9144 m
10. Foot	1 ft = 0.3048 m
11. Inch	1 in = 0.0254 m
12. Mile	1 Mile = 1609.344 m = 1.61 km

(b) For mass

1. Pound	1 Ib = 0.4536 kg
2. Slug	1 slug = 14.59 kg
3. Quintal	1 q= 100 kg
4. Metric tone	1 t = 1000kg
5. Atomic mass unit	1 amu = lu = 1.66 × 10-27 kg

(c) For time

1. Minute	1 min = 60 s
2. Hour	1 h = 60 × 60 s
3. Day	1 day = 24 h= 86400 s
4. Year	1 yr = 365.25 days = 3.156 x 107 s
5. Shake	1 shake = 10-8 s

(d) For other quantities

• Litre (for volume) – 1l = 10³ cc = 10^-3 m³
  where cc represents cubic centimeter i.e. cm³.
• Gallon (for volume) – In U.S.A., 1 gallon = 3.7854 l
• Pascal (for pressure) – 1 Pa = 1 Nm^-2
  Pressure exerted by – 1 atm= 1.01 x 10⁵ Pa
  earthΓÇÖs atmosphere
• Bar (for pressure) – 1 bar = 1 atm. = 1.01 x 10⁵ Pa
• Torr (for pressure) – 1 torr = 1 mm of Hg. col. = 133.3 Pa
• Electron volt (for energy/work) – 1 eV = 1.6 x 10^-19 J
• Erg (for energy/ work) – 1 erg = 10^-7 J
• Kilowatt hour (for energy) – 1 kWh = 3.6 x 10⁶ J
• Horse Power (for power) – 1 hp = 746 W Γëê \(\frac{3}{4}\) KW
• Diopter (for power of a lens) – 1 D = 1 m^-1
• Degree (for angle) – 1┬░ = \(\frac{\pi}{180}\) rad

Just take help from the website Physicscalc.Com and access the Physics Formula Sheet & Tables existing to have a clear idea of the related concepts.