Vector Formulas
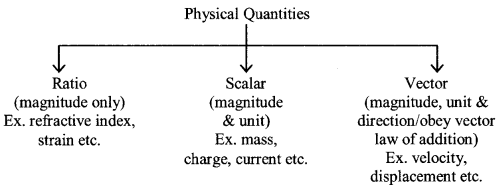
A vector is an object having both direction and magnitude. We have listed some of the Important Formulas for Vector on this page. The Cheat Sheet for Vectors covers concepts such as Graphical Method, Mathematical Method, Application of Vector in Physics. To know more about related topics we have mentioned the Physics Formulas here. Have a quick look at the Formulas Sheet of Vectors covering everything right from basic to advanced level.
List of Formulas for Vectors
Types Of Vector
- Zero vector, \(|\overrightarrow{\mathrm{A}}|\) = 0
- Proper vector, \(|\overrightarrow{\mathrm{A}}|\) Γëá 0
- Like vector → same direction and same sense
- Unlike vector → not same sense
- Equal vector → same magnitude, same direction and same sense
- Negative vector → same magnitude but opposite direction
- Unit vector (vector of unit magnitude) → \(\hat{\mathrm{A}}=\frac{\overrightarrow{\mathrm{A}}}{|\overrightarrow{\mathrm{A}}|}\)
Note – \(\hat{i}, \hat{j} \text { and } \hat{k}\) are the unit vectors in the direction of x, y and z axis.
Representation Of Vector
\(\overrightarrow{\mathrm{A}}\) = \(A_{x} \hat{i}+A_{y} \hat{j}+A_{z} \hat{k}\)
Magnitude = \(|\vec{A}|=\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}\)
Graphical method:
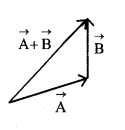
If \(\overrightarrow{\mathrm{A}}=\mathrm{A}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{A}_{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{A}_{\mathrm{z}} \hat{\mathrm{k}}\)
and \(\overrightarrow{\mathrm{B}}=\mathrm{B}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{B}_{\mathrm{y}} \hat{\mathrm{j}}+\mathrm{B}_{\mathrm{z}} \hat{\mathrm{k}}\)
then \(\overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) = (Ax + Bx)\(\hat{\mathrm{i}}\) + (Ay + By)\(\hat{\mathrm{j}}\) + (Az + Bz)\(\hat{\mathrm{k}}\)
R = \(|\vec{A}+\vec{B}|=\sqrt{\left(A_{x}+B_{x}\right)^{2}+\left(A_{y}+B_{y}\right)^{2}+\left(A_{z}+B_{z}\right)^{2}}\)
Note: More than two vector also can be added similar to the above method.
Mathematical method:
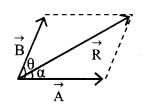
If \(|\overrightarrow{\mathrm{A}}|\) = A and \(|\overrightarrow{\mathrm{B}}|\) = B
θ → angle between \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\)
then R = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
tan ╬▒ = \(\frac{B \sin \theta}{A+B \cos \theta}\)
Scalar Product
- \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = AB cos ╬╕
- \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\)
- \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) = AxBx + AyBy + AzBz
- \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{A}}\) = A2
- \(\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1\)
- \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}=0\)
- \(\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{i}=0\)
⊥ condition
Vector Product
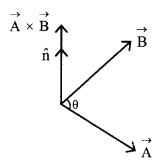
- \(\vec{A} \times \vec{B}\) = AB sin ╬╕ \(\hat{\mathrm{n}}\)
- \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=-\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{A}}\)
- \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\) = 0, || condition
- \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
\mathrm{A}_{\mathrm{x}} & \mathrm{A}_{\mathrm{y}} & \mathrm{A}_{\mathrm{z}} \\
\mathrm{B}_{\mathrm{x}} & \mathrm{B}_{\mathrm{y}} & \mathrm{B}_{\mathrm{z}}
\end{array}\right|\)
= \(\hat{\mathrm{i}}\) (AyBz – AzBy) + \(\hat{\mathrm{j}}\) (AzBx – AxBz)+ \(\hat{\mathrm{k}}\) (AxBy – AyBy)
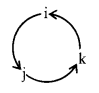
- \(\hat{\mathrm{i}} \times \hat{\mathrm{i}}=\hat{\mathrm{j}} \times \hat{\mathrm{j}}=\hat{\mathrm{k}} \times \hat{\mathrm{k}}=0\)
- \(\hat{\mathrm{i}} \times \hat{\mathrm{j}}=\hat{\mathrm{k}}, \hat{\mathrm{j}} \times \hat{\mathrm{k}}=\hat{\mathrm{i}}, \hat{\mathrm{k}} \times \hat{\mathrm{i}}=\hat{\mathrm{j}}\)
Direction Cosines
Direction cosines:
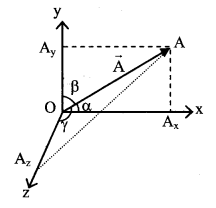
cos ╬▒, cos ╬▓ and cos ╬│ are called direction cosines in x direction, y direction and z direction respectively
cos a = \(\frac{A_{x}}{A}\), cos ╬▓ = \(\frac{A_{y}}{A}\) and cos ╬│ = \(\frac{A_{z}}{A}\) A A ‘A
- cos2 ╬▒ + cos2 ╬▓ + cos2 ╬│ = 1
- sin2 ╬▒ + sin2 ╬▓ + sin2 ╬│ = 2
Application Of Vector In Physics
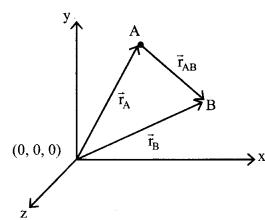
(1) Position vector (\(\vec{r}\)) of point w.r.t. origin (x, y, z): – \(\vec{r}\) = \(x \hat{i}+y \hat{j}+z \hat{k}\)
(2) Displacement vector \(\left(\overrightarrow{\mathrm{r}}_{\mathrm{AB}}\right)\) from point A (x1, y1, z1) to B (x2, y2, z2) \(\overrightarrow{\mathrm{r}}_{\mathrm{AB}}=\overrightarrow{\mathrm{r}}_{\mathrm{B}}-\overrightarrow{\mathrm{r}}_{\mathrm{A}}\) = (x2 – x1)\(\hat{\mathrm{i}}\) + (y2 – y1 )\(\hat{\mathrm{j}}\) + (z2 – z1)\(\hat{\mathrm{k}}\)
(3) Relative velocity: \(\overrightarrow{\mathrm{V}}_{\mathrm{AB}}=\overrightarrow{\mathrm{V}}_{\mathrm{B}}-\overrightarrow{\mathrm{V}}_{\mathrm{A}}\)
Example of dot product
Work: W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{r}}\), Power P = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}\)
ΦE = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\), ΦB = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\)
Example of cross product
\(\overrightarrow{\mathrm{v}}=\vec{\omega} \times \overrightarrow{\mathrm{v}}, \overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{P}}, \quad \vec{\tau}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{F}},\)
\(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
- \(\overrightarrow{\mathrm{v}}=\mathrm{d} \overrightarrow{\mathrm{r}} / \mathrm{dt}, \overrightarrow{\mathrm{a}}=\mathrm{d} \overrightarrow{\mathrm{v}} / \mathrm{dt}\)
- Lorentz force: \(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
- Area of a triangle: \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)
- Area of a parallelogram: \(|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)
- Volume of a parallelepiped: \(\overrightarrow{\mathrm{A}} \cdot(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{C}})\)
- Gradient operator: ∇ = \(\hat{\mathrm{i}} \frac{\partial}{\partial \mathrm{x}}+\hat{\mathrm{j}} \frac{\partial}{\partial \mathrm{y}}+\hat{\mathrm{k}} \frac{\partial}{\partial \mathrm{z}}\) Ex. \(\overrightarrow{\mathrm{E}}\) = -∇Φ
Grab the opportunity to get all the Physics Concepts Formulas along with Vectors Formulae at one go from Physicscalc.Com and clarify all your queries.